Round 353 D. Построение дерева

Васе задали по информатике сложную задачу. К сожалению, Вася не умеет программировать и не смог найти решение в Интернете. Поэтому он обратился за помощью к Вам.

У нас есть последовательность a из n различных чисел, с помощью которой строится бинарное дерево поиска. Опишем правила построения формально.

1. Первое число a₁ становится корнем дерева.

2. Последовательно добавляются все элементы a₂, a₃, ..., a_n. При добавлении элемента a_i выполняется спуск по дереву от корня вниз, по следующим правилам:

· Изначально текущей вершиной является корень.

· Если значение a_i больше значения в текущем элементе, то правый сын текущей вершины становится текущей вершиной. В противном случае текущей вершиной становится левый сын.

· В момент когда требуемый переход в сына невозможен (то есть такой сын отсутствует) создаётся новая вершина, в которую записывается число a_i. Эта вершина становится соответствующим сыном текущей вершины.

Вход. В первой строке входных данных записано целое число n (2 ≤ n ≤ 100 000) – количество элементов в последовательности a.

Во второй строке записаны n различных целых чисел a_i (1 ≤ a_i ≤ 10⁹) – исходная последовательность.

Выход. Выведите n – 1 число. Для всех i > 1 выведите значение, записанное в вершине являющей предком вершины с числом a_i.

Пример входа 1	Пример выхода 1
3 1 2 3	1 2
Пример входа 2	Пример выхода 2
5 4 2 3 1 6	4 2 2 4

РЕШЕНИЕ

структуры данных - дерево

Анализ алгоритма

В случае непосредственного построения бинарного дерева получим Time Limit.

Пусть текущим добавляемым в дерево числом является x. Среди уже добавленных чисел найдем такое наибольшее l и такое наименьшее r, что l < x < r (одно из таких чисел может отсутствовать, но при этом идея решения не меняется). Такие l и r можно найти при помощи бинарного поиска.

Для сохранения свойства отсортированности x должно быть либо правым потомком вершины l, либо левым потомком вершины r. Предположим, что l не имеет правого потомка, а r левого. Тогда lca(l, r) не совпадает ни с l, ни с r. Значит l < lca(l, r) < r, что невозможно, так как l максимально а r минимально. Следовательно либо l имеет правого потомка, либо r левого. То есть позиция (и предок) для x определяется однозначно.

Для каждой вершины v в left[v] будем запоминать ее левого сына , а в right[v] – ее правого. В качестве структур данных для left и right выберем отображение map.

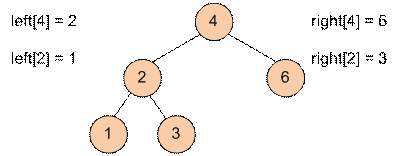
Пример

Дерево из второго теста имеет вид:

Реализация алгоритма

#include <cstdio>

#include <set>

#include <map>

using namespace std;

set<int> numbers;

set<int>::iterator it;

map<int, int> left;

map<int, int> right;

int main(void)

{

int n, v;

scanf("%d %d",&n,&v);

numbers.insert(v);

for (int i = 0; i < n - 1; i++)

{

scanf("%d",&v);

it = numbers.upper_bound(v);

int result;

if (it != numbers.end() && left.count(*it) == 0)

{

left[*it] = v;

result = *it;

} else

{

it--;

right[*it] = v;

result = *it;

}

numbers.insert(v);

printf("%d",result);

if (i == n - 2) printf("\n");

else printf(" ");

}

}